Wie können wir die Größe eines fernen Sterns bestimmen? Einfach mit einem guten Teleskop hinzuschauen und unter Berücksichtigung seiner Entfernung die Größe abzuschätzen, ist schlicht und einfach ungenau und nicht zielführend. Wir brauchen andere Methoden!
Dazu sammeln wir alle Informationen, die wir über den Stern erfahren können - und all diese Informationen stecken in seinem ausgesandten Licht. Abermals haben wir nicht mehr (und nicht weniger) als das. Einen Großteil unseres Wissens über die Himmelskörper übermittelte uns nur das Licht. Es ist schon faszinierend, dass wir uns ein Bild von Orten im Weltall machen können, an denen natürlich noch niemand von uns war und zu denen wir auch wohl niemals gelangen können. Das alles ist möglich durch den wissenschaftlichen und technischen Fortschritt und durch die Macht des logischen Denkens.
Heute soll es darum gehen, wie man den Radius ferner Sterne, die uns ja normalerweise nur als Punkte ohne Ausdehnung am Himmel erscheinen, mit geschickten Überlegungen herausfinden kann.
Ein Blog über die physikalische Umwelt von Sebastian Templ
Samstag, 28. September 2013
Samstag, 21. September 2013
Die Sonne schrumpft
...und zwar gewaltig schnell, wenn man in irdischen Dimensionen denkt.
Im Kern der Sonne passieren ja ständig nukleare Fusionen, bei denen Wasserstoff in Helium umgewandelt wird. Dabei werden - grob gesagt - aus vier Wasserstoffatomen ein Heliumatom. Der Grund, warum die Sonne so heiß ist, ist folgender: Nimmt man die einzelnen Bestandteile, die ein Heliumatom aufbauen (zwei Protonen und zwei Neutronen), "wiegt" man sie einzeln ab und zählt ihre Massen dann zusammen, so beobachtet man, dass diese Summe der einzelnen Massen größer ist als die Masse eines Heliumatoms. Wie ist das möglich? Warum werden unsere atomaren "Grundbausteine" plötzlich leichter, wenn man sie zu einem Heliumatom kombiniert?
Zwischen "Ausgangsstoffen" und "Endprodukten" gibt es also einen Massenunterschied. Kann man sagen, es ist Masse "verloren" gegangen? Ist Masse nicht eine Art Erhaltungsgröße, sodass sie nie einfach verschwinden oder erscheinen kann? - Die Antwort ist: Nein, die Masse wird nur in der klassischen, newtonschen Physik erhalten. Wie Einstein herausgefunden hat, kann Masse in Energie umgewandelt werden. Masse und Energie sind über seine berühmte Masse-Energie-Äquivalenzformel E = Δmc2 miteinander eng verbunden. (Wir schreiben hier "Delta-m" - also Δm - anstatt einfach nur m, was verdeutlichen soll, dass wir uns hier mit Massendifferenzen beschäftigen.) Bei der Kernfusion geht also keine Masse einfach so verloren, sondern sie wird in Energie umgewandelt. Es gilt also eine Art universellerer Erhaltungssatz.
Diese Energie wird abgestrahlt, wandert vom Sonnenkern mehrere 100.000 Jahre zur Sonnenoberfläche und danach etwa acht Minuten lang zu uns auf die Erde, wo sie unsere Eislutscher oder - fast noch schlimmer - unser Bier erwärmt. (Hat sich das ganze also ausgezahlt?) ;-)
Im Kern der Sonne passieren ja ständig nukleare Fusionen, bei denen Wasserstoff in Helium umgewandelt wird. Dabei werden - grob gesagt - aus vier Wasserstoffatomen ein Heliumatom. Der Grund, warum die Sonne so heiß ist, ist folgender: Nimmt man die einzelnen Bestandteile, die ein Heliumatom aufbauen (zwei Protonen und zwei Neutronen), "wiegt" man sie einzeln ab und zählt ihre Massen dann zusammen, so beobachtet man, dass diese Summe der einzelnen Massen größer ist als die Masse eines Heliumatoms. Wie ist das möglich? Warum werden unsere atomaren "Grundbausteine" plötzlich leichter, wenn man sie zu einem Heliumatom kombiniert?
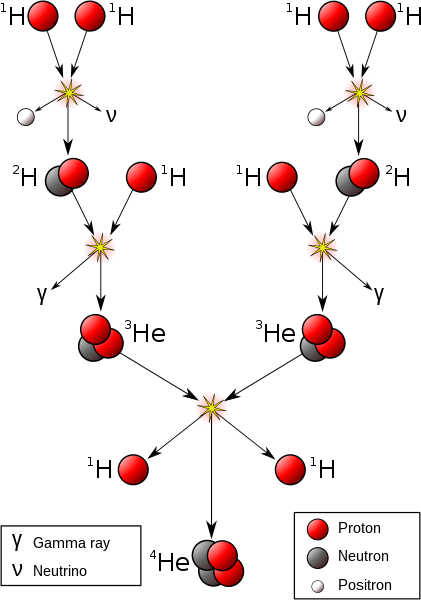 |
| Schematischer Ablauf der Proton-Proton-Reaktion (Quelle: https://commons.wikimedia.org/wiki/File:FusionintheSun.svg) |
Zwischen "Ausgangsstoffen" und "Endprodukten" gibt es also einen Massenunterschied. Kann man sagen, es ist Masse "verloren" gegangen? Ist Masse nicht eine Art Erhaltungsgröße, sodass sie nie einfach verschwinden oder erscheinen kann? - Die Antwort ist: Nein, die Masse wird nur in der klassischen, newtonschen Physik erhalten. Wie Einstein herausgefunden hat, kann Masse in Energie umgewandelt werden. Masse und Energie sind über seine berühmte Masse-Energie-Äquivalenzformel E = Δmc2 miteinander eng verbunden. (Wir schreiben hier "Delta-m" - also Δm - anstatt einfach nur m, was verdeutlichen soll, dass wir uns hier mit Massendifferenzen beschäftigen.) Bei der Kernfusion geht also keine Masse einfach so verloren, sondern sie wird in Energie umgewandelt. Es gilt also eine Art universellerer Erhaltungssatz.
Diese Energie wird abgestrahlt, wandert vom Sonnenkern mehrere 100.000 Jahre zur Sonnenoberfläche und danach etwa acht Minuten lang zu uns auf die Erde, wo sie unsere Eislutscher oder - fast noch schlimmer - unser Bier erwärmt. (Hat sich das ganze also ausgezahlt?) ;-)
Montag, 16. September 2013
Smarter Every Day feiert ein Jubiläum!
Destin vom YouTube-Kanal Smarter Every Day hat vor kurzem die hundertste Folge herausgebracht, in welcher er sein Jubiläum feiert. Es ist ein schönes Video, welches ich euch unbedingt empfehlen möchte.
(Abgesehen davon finde ich, dass Destin eine sehr interessante und sympathische Persönlichkeit ist. Gratulation auch meinerseits zu hundert Folgen Smarter Every Day!)
Vielleicht bekommt der eine oder andere Appetit, sich auch andere seiner Videos anzusehen und smarter even this day zu werden. ;-)
Samstag, 14. September 2013
Entwicklung der Quantenphysik XI: Worum ging es nun eigentlich? - Ein Resümee
Puh... es war ein langer Weg bis hierher!
Angefangen hat alles mit dem Problem der Ultraviolett-Katastrophe der Hohlraumstrahlung und Planck's Quantenhypothese. Licht war plötzlich nicht mehr eine Welle, sondern bekam einen Teilchencharakter. Dann ging es richtig los, als Louis de Broglie vorschlug, auch "Teilchen" (wie z. B. Elektronen) durch Materiewellen zu beschreiben. Die Folgen waren weitreichend: Man entdeckte, dass sich die Welt auf fundamentaler Ebene nur mehr durch Wahrscheinlichkeiten ausdrücken lässt. Außerdem gibt es prinzipielle Grenzen in der Bestimmbarkeit gemäß der Heisenberg'schen Unbestimmtheitsrelation. Das klassisch-deterministische Universum von Newton und seinen Zeitgenossen, das bereits durch Einsteins Relativitätstheorie in seinen Grundfesten erschüttert wurde, entpuppte sich als eine zu oberflächliche Naturbeschreibung. Auch in der Atomvorstellung gab es revolutionäre Erkenntnisse - so sind die Elektronenbahnen um den Atomkern in Bohrs Atommodell gequantelt, sodass es für die Elektronen "verbotene" Bereiche gibt, in denen sie sich nicht aufhalten können. Der Doppelspaltversuch mit all seinen Variationen zeigt wohl am deutlichsten, welche Kuriositäten in der mikroskopischen Quantenwelt herrschen: Man kann ihn in Begriffen der klassischen Physik (also unserer "Hausverstandsphysik") nicht erklären.
Über viele Jahre haben wir mehrere Interpretationen dieser für uns so absonderlich wirkenden Quantenmechanik erarbeitet, die sich bislang als konsistent mit der Natur erwiesen haben. Die am meisten verbreitete und in den meisten Lehrstätten unterrichtete ist die sog. "Kopenhagener Interpretation". Sie erlaubt uns, die Natur mit bisher unerreichter Genauigkeit zu beschreiben und hat nebenbei eine Revolution im technologischen Fortschritt ausgelöst. Moderne Technik wäre ohne die grundlegenden Erkenntnisse vieler Wissenschafter des vorherigen Jahrhunderts nicht denkbar!
Wie wir in dieser Artikelserie gesehen haben, kann die Quantenphysik ehemals paradoxe Phänomene, wie z. B. die Ultraviolett-Katastrophe, die Stabilität der Atome, die Elektronenbeugung oder den photoelektrischen Effekt, zufriedenstellend erklären. (Es gibt eine Erweiterung dieser "neuen Physik", die sog. "Quantenelektrodynamik" oder kurz "QED". Die Quantenelektrodynamik befindet sich bislang in vollkommener Übereinstimmung mit den Experimenten. Obwohl man sie ohne jahrelanger Beschäftigung mit Mathematik und Physik wohl nicht vollständig verstehen kann, möchte ich Interessierten Richard Feynmans Buch "QED: Die seltsame Theorie des Lichts und der Materie" ans Herz legen. Feynman beschreibt dieses/sein Konzept der QED auf eine Weise, die so anschaulich ist, dass ich sogar etwas damit anfangen konnte, als ich das Buch bereits vor meinem Physikstudium gelesen hatte.)
Die Quantenphysik vermag also alle Erscheinungen der Elektronenhüllen der Atome und damit die Atom- und Molekülphysik auf befriedigende Weise zu beschreiben. Erst bei der Untersuchung der Kernstruktur und der Elementarteilchen wird ihre Beschreibung lückenhaft. (Es ist übrigens auch noch nicht gelungen, allgemeine Relativitätstheorie, also die Gravitation, und die Quantenphysik erfolgreich zu vereinen. Falls das jemandem von euch eines Tages gelingt, könnt ihr wohl gleich die Koffer packen, um euch den Nobelpreis aus Stockholm abzuholen.)
Doch was ist nun eigentlich das Besondere an der Quantenphysik? Was ist ihre "zentrale Aussage"?
Wir haben bisher ja sehr viele kuriose Phänomene kennengelernt, sodass wahrscheinlich untergegangen ist, was die Quantenphysik eigentlich auszeichnet.
In vielen Quellen wird die Heisenbergsche Unbestimmtheitsrelation als die grundlegende Aussage der Quantenphysik bezeichnet. Das stimmt nicht, denn sobald man akzeptiert, dass man "Teilchen" durch Wellen beschreiben kann, folgt die Unbestimmtheitsrelation (und zwar aus dem klassischen Fourier-Theorem). Obwohl diese Relation weitreichende und philosophische Fragen aufwirft, ist sie also in dem Sinne nicht "so besonders", wie einem oftmals glaubhaft gemacht wird.
Angefangen hat alles mit dem Problem der Ultraviolett-Katastrophe der Hohlraumstrahlung und Planck's Quantenhypothese. Licht war plötzlich nicht mehr eine Welle, sondern bekam einen Teilchencharakter. Dann ging es richtig los, als Louis de Broglie vorschlug, auch "Teilchen" (wie z. B. Elektronen) durch Materiewellen zu beschreiben. Die Folgen waren weitreichend: Man entdeckte, dass sich die Welt auf fundamentaler Ebene nur mehr durch Wahrscheinlichkeiten ausdrücken lässt. Außerdem gibt es prinzipielle Grenzen in der Bestimmbarkeit gemäß der Heisenberg'schen Unbestimmtheitsrelation. Das klassisch-deterministische Universum von Newton und seinen Zeitgenossen, das bereits durch Einsteins Relativitätstheorie in seinen Grundfesten erschüttert wurde, entpuppte sich als eine zu oberflächliche Naturbeschreibung. Auch in der Atomvorstellung gab es revolutionäre Erkenntnisse - so sind die Elektronenbahnen um den Atomkern in Bohrs Atommodell gequantelt, sodass es für die Elektronen "verbotene" Bereiche gibt, in denen sie sich nicht aufhalten können. Der Doppelspaltversuch mit all seinen Variationen zeigt wohl am deutlichsten, welche Kuriositäten in der mikroskopischen Quantenwelt herrschen: Man kann ihn in Begriffen der klassischen Physik (also unserer "Hausverstandsphysik") nicht erklären.
| (Credit: Zach Weiner, SMBC) |
Wie wir in dieser Artikelserie gesehen haben, kann die Quantenphysik ehemals paradoxe Phänomene, wie z. B. die Ultraviolett-Katastrophe, die Stabilität der Atome, die Elektronenbeugung oder den photoelektrischen Effekt, zufriedenstellend erklären. (Es gibt eine Erweiterung dieser "neuen Physik", die sog. "Quantenelektrodynamik" oder kurz "QED". Die Quantenelektrodynamik befindet sich bislang in vollkommener Übereinstimmung mit den Experimenten. Obwohl man sie ohne jahrelanger Beschäftigung mit Mathematik und Physik wohl nicht vollständig verstehen kann, möchte ich Interessierten Richard Feynmans Buch "QED: Die seltsame Theorie des Lichts und der Materie" ans Herz legen. Feynman beschreibt dieses/sein Konzept der QED auf eine Weise, die so anschaulich ist, dass ich sogar etwas damit anfangen konnte, als ich das Buch bereits vor meinem Physikstudium gelesen hatte.)
Die Quantenphysik vermag also alle Erscheinungen der Elektronenhüllen der Atome und damit die Atom- und Molekülphysik auf befriedigende Weise zu beschreiben. Erst bei der Untersuchung der Kernstruktur und der Elementarteilchen wird ihre Beschreibung lückenhaft. (Es ist übrigens auch noch nicht gelungen, allgemeine Relativitätstheorie, also die Gravitation, und die Quantenphysik erfolgreich zu vereinen. Falls das jemandem von euch eines Tages gelingt, könnt ihr wohl gleich die Koffer packen, um euch den Nobelpreis aus Stockholm abzuholen.)
Doch was ist nun eigentlich das Besondere an der Quantenphysik? Was ist ihre "zentrale Aussage"?
Wir haben bisher ja sehr viele kuriose Phänomene kennengelernt, sodass wahrscheinlich untergegangen ist, was die Quantenphysik eigentlich auszeichnet.
In vielen Quellen wird die Heisenbergsche Unbestimmtheitsrelation als die grundlegende Aussage der Quantenphysik bezeichnet. Das stimmt nicht, denn sobald man akzeptiert, dass man "Teilchen" durch Wellen beschreiben kann, folgt die Unbestimmtheitsrelation (und zwar aus dem klassischen Fourier-Theorem). Obwohl diese Relation weitreichende und philosophische Fragen aufwirft, ist sie also in dem Sinne nicht "so besonders", wie einem oftmals glaubhaft gemacht wird.
Freitag, 13. September 2013
Zu Recht: Links - September 2013 (1/2)
Die Einträge, die mit einem "≤" eingeleitet werden, sind besonders sehenswert! Allen, denen die folgende Liste etwas zu lang ist, möchte ich bei ihrer Wahl damit ein bisschen unter die Arme greifen. ;-)
Hunderte alter Link-Empfehlungen sind hier zu finden.
Samstag, 7. September 2013
Entwicklung der Quantenphysik X: Der verblüffende Versuch (2/2)
Das letzte Mal habe ich über eines der berühmtesten physikalischen Experimente aller Zeiten geschrieben. Der Young'sche Doppelspalt-Versuch und seine verschiedenen Variationen zeigen tatsächlich sehr demonstrativ, welche kuriosen Überraschungen die Quantenmechanik für uns bereithält, wenn man im Rahmen der klassischen Physik denkt.
Wir haben gedanklich bereits makroskopische Teilchen (Farbtröpfchen) und Licht (in Form von Photonen) durch einen Doppelspalt geschickt. Dabei wurde hoffentlich der Unterschied zwischen der Intensitätsverteilung klassischer Teilchen hinter dem Spalt und der Intensitätsverteilung quantenmechanischer Teilchen (in unserem Fall Photonen) deutlich.
Die Intensitäten der Teilchenstrahlen durch die einzelnen Spalten werden im klassischen Fall einfach zusammengezählt und ergeben somit ganz intuitiv die Gesamtintensität. Man könnte auch sagen: |ψ(x=D, y)|2 = |ψ1|2 + |ψ2|2. (Das ψ bedeutet die Wellenfunktion, mit der wir die Teilchen beschreiben. Es handelt sich hierbei um eine Wahrscheinlichkeitsdichte. Im klassischen Fall kann man statt dieser etwas komplizierten Schreibweise einfach ganz normal die Intensitäten der Teilchen durch die einzelnen Spalte addieren: Igesamt = I1 + I2.)
Im Falle von einzelnen Photonen beobachten wir Interferenzen, wenn beide Spalte offen sind! Die Intensität ist plötzlich vom Winkel abhängig, wie man aus dieser Gleichung - durch den Kosinus - ablesen kann (mehr dazu im vorhergehenden Artikel!):
|ψ(x=D, y)|2 = |ψ1+ψ2|2 = |ψ1|2 + |ψ2|2 + (A2/r2)·cos k(r1-r2)
Sobald einer der beiden Spalte geschlossen wird, beobachten wir wieder die klassische Intensitätsverteilung.
Die folgenden zwei Abbildungen sollen den Unterschied noch einmal verdeutlichen:
| Doppelspalt-Experiment (Credit: Koantum, svg version by Trutz Behn) |
Wir haben gedanklich bereits makroskopische Teilchen (Farbtröpfchen) und Licht (in Form von Photonen) durch einen Doppelspalt geschickt. Dabei wurde hoffentlich der Unterschied zwischen der Intensitätsverteilung klassischer Teilchen hinter dem Spalt und der Intensitätsverteilung quantenmechanischer Teilchen (in unserem Fall Photonen) deutlich.
Die Intensitäten der Teilchenstrahlen durch die einzelnen Spalten werden im klassischen Fall einfach zusammengezählt und ergeben somit ganz intuitiv die Gesamtintensität. Man könnte auch sagen: |ψ(x=D, y)|2 = |ψ1|2 + |ψ2|2. (Das ψ bedeutet die Wellenfunktion, mit der wir die Teilchen beschreiben. Es handelt sich hierbei um eine Wahrscheinlichkeitsdichte. Im klassischen Fall kann man statt dieser etwas komplizierten Schreibweise einfach ganz normal die Intensitäten der Teilchen durch die einzelnen Spalte addieren: Igesamt = I1 + I2.)
Im Falle von einzelnen Photonen beobachten wir Interferenzen, wenn beide Spalte offen sind! Die Intensität ist plötzlich vom Winkel abhängig, wie man aus dieser Gleichung - durch den Kosinus - ablesen kann (mehr dazu im vorhergehenden Artikel!):
|ψ(x=D, y)|2 = |ψ1+ψ2|2 = |ψ1|2 + |ψ2|2 + (A2/r2)·cos k(r1-r2)
Sobald einer der beiden Spalte geschlossen wird, beobachten wir wieder die klassische Intensitätsverteilung.
Die folgenden zwei Abbildungen sollen den Unterschied noch einmal verdeutlichen:
Intesitätsverteilung für klassische Teilchen hinter dem Doppelspalt
|
| Intensitätsverteilung von Licht - beide Spalte offen - hinter dem Doppelspalt (Quelle: http://commons.wikimedia.org/wiki/File:Slit_double_57_8.svg) |
Das Bisherige habe ich ja bereits im letzten Artikel erzählt. Wem das hier zu schnell gegangen ist, der kann dort nachschlagen.
Versuchen wir etwas Neues, indem wir heute Elektronen durch den Doppelspalt schicken!
Abonnieren
Kommentare (Atom)
