In diesem Artikel werde ich mich allerdings weniger mit der Erforschung der Sonne in der Geschichte beschäftigen, sondern mich auf moderne Messmethoden konzentrieren, um zu zeigen, wie wir die Eigenschaften der Sonne in Erfahrung bringen können.
Abschließend gibt's dann noch zwei wirklich sehenswerte Videos. ;-)
Vorhergehende Artikel (dieser Artikel greift auf diese zurück):
- Helligkeit und Leuchtkraft
- Temperatur eines Sterns
- Chemische Zusammensetzung
- Radius eines Sterns
- Masse eines Sterns
VI) Beispiel Sonne:
Zum Abschluss meiner Blogartikel-Reihe "Sternenlicht 'lesen'" werde ich also die Erkenntnisse der vorherigen Artikel auf die Sonne anwenden und kurz zeigen, wie man auf die Eigenschaften "unseres" Sterns kommt.
Die Werte in den folgenden Rechnungen werden oft gerundet, sodass die Ergebnisse ein bisschen von den tatsächlichen Werten abweichen können. Der Unterschied zum "richtigen" Ergebnis ist allerdings für unsere Zwecke vernachlässigbar gering. Immerhin wollen wir nur in Erfahrung bringen, mit welch großem/heißen/etc. Himmelskörper wir es hier zu tun haben - deshalb sind z.B. Nachkommastellen nicht wirklich von Belang.
1) Berechnung der Leuchtkraft:
Folgende Überlegung führt uns zu einer einfachen Berechnung der Leuchtkraft der Sonne:
Wir nehmen an, dass die Sonne ihre Energie in alle Richtungen gleichermaßen abstrahlt ("Isotropie"). Die Strahlungsleistung sei also auf der gesamten Sonnenoberfläche gleich. Bewegen wir uns mit einem gewissen Abstand um die Sonne, messen wir in dieser Entfernung immer das gleiche. Wir stellen uns also eine riesige Kugel vor, deren Mittelpunkt die Sonne darstellt. Auf der Kugeloberfläche ist die von der Sonne kommende Energie stets gleich. Als nächsten Schritt wählen wir den Radius der Kugel so, dass er der Entfernung zwischen Sonne und Erde entspricht (also 1 AE beträgt) - das sind etwa 150 Mio. km.
Wir brauchen also nur zu messen, wie viel Energie pro Sekunde und Quadratmeter bei der Erde ankommt. Um die störenden Effekte der Erdatmosphäre auszuschalten, überlassen wir die Messung z.B. einem Satelliten außerhalb der Atmosphäre. Dieser misst einen Wert von 1370 W/m². Diesen Wert nennt man auch die Solarkonstante.
Da man den Raum zwischen Sonne und Erde für unsere Zwecke ohne weiteres als "leer" bezeichnen kann, verliert das Licht der Sonne auf seinem Weg zur Erde quasi keine Energie. Auf unserer imaginären Kugeloberfläche misst man somit auf jedem einzelnen m² diesen Wert der Solarkonstante. Alles zusammen - "alle m² zusammen" - ergibt die tatsächliche Strahlungsleistung der Sonne.
Zur Berechnung dient die Formel (mehr dazu im ersten Artikel der Reihe)
L.....Leuchtkraft
f......Energiefluss (Energie pro Zeit, "Strahlungsleistung")
R.....Abstand zw. Stern und Erde
Ω.....Ist die Strahlungsquelle (der Stern) isotrop - d.h. in alle Richtungen gleichermaßen strahlend - gilt Ω = 4π, weil sich die gesamte Energie auf eine Kugeloberfläche mit dem Radius R verteilt.
Die konkrete Berechnung im Fall der Sonne sieht also so aus:
2) Temperatur der Sonne:
Zur Bestimmung der Temperatur müssen wir das Sonnenspektrum analysieren:
 |
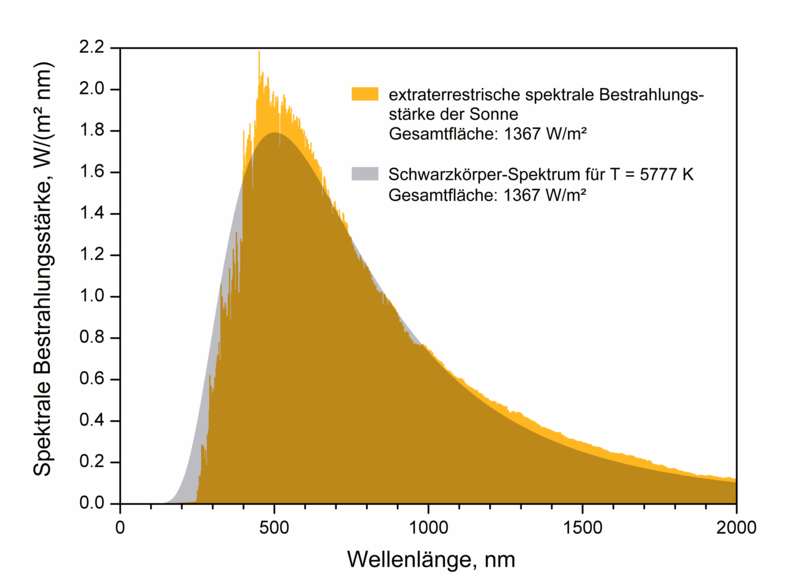| Sonnenspektrum (Quelle: https://commons.wikimedia.org/wiki/File:EffectiveTemperature_300dpi.png) |
Wir sehen, dass die Sonne Licht mit einer Wellenlänge von ca. 500 nm am stärksten abstrahlt.
λmax = 500 nm.
Mit Hilfe des Wien'schen Verschiebungsgesetzes [T = (2,9.10⁻³ m K)/λmax; siehe zweiter Artikel] können wir die Temperatur auf der Sonnenoberfläche berechnen:
3) Chemische Zusammensetzung der Sonnenphotosphäre:
Was es mit den schwarzen Linien (Fraunhoferlinien) im Sonnenspektrum auf sich hat, könnt ihr im dritten Artikel nachlesen.
An dieser Stelle möchte ich nur die folgende Abbildung zeigen, die die auffälligsten Absorptionslinien im Sonnenspektrum eingezeichnet hat.
Die Sonnenatmosphäre besteht zum größten Teil aus Wasserstoff (fast 91 %) und Helium (fast 9 %). Man findet auch Spuren von Sauerstoff, Kohlenstoff, Neon, Stickstoff, Eisen, Magnesium, Silizium und Schwefel.
 |
| Auffälligste Absorptionslinien im Sonnenspektrum. Details zur dieser Bezeichnung (von Fraunhofer) und aktuelleres Spektrum: (Quelle: http://www.leifiphysik.de/themenbereiche/atomarer-energieaustausch/lb/fraunhoferlinien-details) |
4) Größe der Sonne:
Um den Radius der Sonne bestimmen zu können, halten wir uns ans "Stefan-Boltzmann-Gesetz" (siehe vierter Artikel).
Dieses lautet:
5) Masse der Sonne:
Wie man die Masse der Sonne berechnet, habe ich im Grunde schon im fünften Artikel der Reihe vorweggenommen.
Kurz noch einmal hier zusammengefasst:
Wir kombinieren das dritte Keplersche Gesetz mit dem Gravitationsgesetz und erhalten:
Wir setzen alle bekannten Werte (in SI-Einheiten!) in die Gleichung ein [G ist die Gravitationskonstante 6,67 . 10-11 m³/(kg.s²)] und berechnen uns M.
Abschließend führe ich hier noch ein paar Zeilen an, die ich kurzerhand von Wikipedia kopiert habe, um einen kleinen Eindruck von den Größenordnungen anderer Sterne zu bekommen:
Der Wertebereich einiger Zustandsgrößen überdeckt viele Größenordnungen. Die Oberflächentemperaturen von Hauptreihensternen reichen von etwa 2200 K bis 45.000 K, ihre Massen von 0,07 bis 120 Sonnenmassen und ihre Radien von 0,1 bis 25 Sonnenradien. Rote Riesen sind deutlich kühler und können so groß werden, dass die komplette Erdbahn in ihnen Platz hätte, bei VY Canis Majoris sogar die des Saturns. Weiße Zwerge haben Temperaturen bis zu 100.000 K, sind aber nur so klein wie die Erde, obwohl ihre Masse mit der der Sonne vergleichbar ist.
Wir sehen also, dass unsere Sonne mit ihren oben berechneten Werten nicht außergewöhnlich ist. Dass es da draußen im Universum sogar noch um viele Größenordnungen größere Sterne gibt, zeigt dieses folgende, sehr sehenswerte Video eindrucksvoll:
Und um endlich einmal ein Gefühl dafür zu bekommen, wie weit die Planeten in unserem Sonnensystem wirklich voneinander entfernt sind (dies wird nämlich in fast keinem (Schul-)buch erwähnt, geschweige denn dargestellt), empfehle ich dieses unterhaltsame Video mit unserem Bill Nye. Die Dimensionen innerhalb unseres Sonnensystems sind so unbegreiflich groß, dass einem leicht mal schwindlig wird, wenn man versucht, sich die Größe einer Galaxie bzw. des sichtbaren Universums vorzustellen.
Andere Artikel dieser Serie:
- Helligkeit und Leuchtkraft
- Temperatur eines Sterns
- Chemische Zusammensetzung
- Radius eines Sterns
- Masse eines Sterns
- Beispiel Sonne
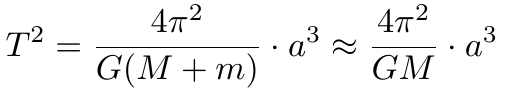
Keine Kommentare:
Kommentar veröffentlichen