Erstaunliches aus unserer sichtbaren Blase des Universums: Sternenlicht "lesen" II

Unser Wissen über das Universum ist seit Beginn der Wissenschaft (anfangs wohl eher der Naturphilosophie) enorm gewachsen. Der permanente Erkenntnisgewinn hält bis heute an.
Um die Natur, ihre Beschaffenheit und Gesetzmäßigkeiten genauer kennenzulernen, muss man sie gründlich beobachten.
Genau das macht die Menschheit seit jeher und hat dabei Großartiges gelernt.

Im diesem Artikel - dem zweiten Teil aus meiner Reihe "Sternenlicht 'lesen'" - konzentriere ich mich abermals auf Informationen, die man aus dem Licht eines Sterns in Erfahrung bringen kann. Ich hoffe, auch diesmal zeigen zu können, auf welch bemerkenswerte Weise wir unser Wissen über weit entferne Sterne und Galaxien erweitern, indem wir nur das von ihnen ausgesandte Licht betrachten.

Vorhergehende Artikel (zum Verständnis dieses Artikels teilweise notwendig):

Helligkeit und Leuchtkraft

II) Temperatur eines Sterns:

Wie misst man Temperatur und Größe eines Sterns, den man womöglich nicht einmal mit freiem Auge sehen kann?
Die auf den ersten Blick knifflige Erklärung entpuppt sich als nicht allzu schwer und durchaus verständlich.

Zuerst muss man wissen, was "Temperatur" eigentlich bedeutet:
Teilchen (also Atome und ihre Bestandteile) kommen niemals zur Ruhe. Sie zittern ständig hin und her. Betrachtet man ein Glas Wasser, welches schon Stunden auf dem Tisch im Wohnzimmer steht, sieht es auch bei genauerer Betrachtung völlig ruhig aus. Das liegt aber nur daran, dass das Auflösungsvermögen unserer Augen viel zu grob ist, um die einzelnen Bestandteile des Wassers (also die H₂O-Moleküle) zu erkennen. Diese Moleküle führen ständig Zitterbewegungen aus und Vertauschen sogar ihre Plätze, indem sie aneinander "vorbeizittern". Wir schalten nun die Klimaanlage im Wohnzimmer ein (Ja, wir haben eine dort.) und kühlen den Raum auf einige Grad unter 0 °C (Ja, unsere Klimaanlage ist ihr Geld echt wert!). Die Zitterbewegungen der Wassermoleküle verlangsamen sich. Bald reichen die Bewegungen nicht mehr aus, um Plätze mit den Nachbarmolekülen zu tauschen. Somit verharrt jedes Molekül mehr oder weniger auf seinem Platz und zittert vor sich hin. Den hier betrachteten Zustand nennen wir "Eis". Wenn wir das gefrorene Wasser wieder erwärmen (Unserer Klimaanlage wurde es wohl zu viel, sie spielt jetzt verrückt und heizt den Raum auf über 100 °C. Spätestens jetzt bin ich froh, dass es sich hier nur um eine fiktive Klimaanlage handelt!) zittern die Teilchen im Wasser immer mehr und mehr. Einige tauschen sogar wieder ihre Plätze (flüssiges Wasser). Nach einer Weile rasen die Moleküle immer schneller umher, sodass sie die benachbarten stoßen und wegschießen. Ihre Zitterbewegungen nehmen nun so viel Platz ein, dass man gar nicht mehr von "fixen" Plätzen innerhalb des Wasserglases reden kann. Das Wasser als ganzes dehnt sich stark aus und verteilt sich im ganzen Raum, weil bald alle Wassermoleküle schnell genug sind (also genug Energie haben), um das flüssige Wasser zu verlassen. Sie schießen förmlich aus der Ansammlung ihrer noch "flüssigen Kollegen". Wir haben jetzt Wasserdampf, den gasförmigen Zustand des Wassers.
Am Beispiel der Aggregatzustände des Wassers kann man die inneren Teilchenbewegungen eines Körpers gut verstehen. Die Summe aller Teilchenbewegungen ist ein Maß für die Temperatur - je stärker die Bewegungen der kleinsten Bestandteile sind umso wärmer ist der Körper.
(Zur Veranschaulichung: Klatscht oft und fest in die Hände. Dabei "schüttelt" ihr die Atome, die die Hände aufbauen. Je fester und öfter ihr klatscht umso wärmer werden eure Hände werden. Kühlen sie danach wieder ab, stoßen sie mit den langsameren Luftmolekülen zusammen, welche dadurch beschleunigt werden. (Bzw. wird Wärme auch durch das vorbeifließende Blut wegtransportiert etc.) Die Wärme "ging" somit von den warmen Händen auf ein kälteres Medium über.)

Auf den Größenordnung der Moleküle und Atome ist die Welt also undurchschaubar chaotisch und hektisch - alles zittert und flimmert, es gibt keine Ruhe. Ständig findet Veränderung statt. Wir können froh sein, dass wir durch unsere Riesigkeit (im Vergleich zu den kleinen Bestandteilen der Natur) die Welt in großen Skalen sehen und dadurch über die unseren Bausteinen zugrunde liegende Hektik hinwegsehen können!

Simulation der Brown'schen Bewegung eines großen Teilchens
(z. B. Staubpartikel in einem Gas)
(Quelle: http://commons.wikimedia.org/wiki/File:Brownian_motion_large.gif)

Aufgrund der permanenten Bewegung der atomaren Teilchen gibt jeder Körper elektromagnetische Strahlung ab, weil bewegte Ladungen eben elektromagnetische Wellen abgeben. ("Strahlung" und "Welle" sind jeweils Ausdrücke für die selbe Sache, kann man sagen.)

Und damit kommen wir schon zur knappen Besprechung des elektromagnetischen Spektrums:
Die untere Abbildung zeigt dieses Spektrum. Man erkennt, dass der für den Menschen sichtbare Bereich relativ klein ist (Der regenbogenfarbene Bereich wurde im Bild hervorgehoben und oberhalb vergrößert dargestellt). Unsere Augen können elektromagnetische Strahlung nur im Wellenlängenbereich von 380 bis 780 nm (Nanometern) oder im Frequenzbereich von ca. 3,8 · 10¹⁴ bis 7,9 · 10¹⁴ Hz (Hertz) sehen. Dass alle anderen Frequenzen (oder Wellenlängen) für uns nicht sichtbar sind, lässt sich evolutionstheoretisch erklären - die Sonne strahlt genau im für uns sichtbaren Bereich am stärksten, auch Atmosphäre und Wasser lassen genau dieses Licht ungehindert durch. Deshalb entwickelten wir uns (genauso wie viele andere Lebewesen) so, dass wir in den Frequenzbereichen, die auf unserem Heimatplaneten am häufigsten vorkommen, am besten sehen. (Nachträglich eingefügte Bemerkung: Die eben beschriebene Tatsache könnte falsch sein, wie Martin Bäker in einem seiner Blogartikel beschreibt!)
Und bevor ich mich mit der Tatsache, dass unser zentraler Stern ein Intensitätsmaximum in seinem Strahlungsspektrum hat, dem Thema der Temperatur von Sternen nähere, empfehle ich, die folgende Abbildung genauer zu betrachten. Es ist ganz interessant, visualisiert zu bekommen, welche Frequenzen für verschiedene Technologien, die unseren Alltag mitbestimmen, verwendet werden.
Je länger die Wellenlänge und je kleiner somit die Frequenz sind, desto energieärmer ist die Strahlung. Kürzere Wellenlängen und höhere Frequenzen bedeuten energiereichere Strahlung. (Zum Vergleich: Hochfrequente Gammastrahlung, die z.B. durch radioaktiven Zerfall entsteht, ist eindeutig energetischer als die langwelligen Runkfunkwellen, die ständig "in der Luft" sind.)

Das elektromagnetische Spektrum (klicken zum Vergrößern!)
(Quelle: http://commons.wikimedia.org/wiki/File:Electromagnetic_spectrum_c.svg)

Jetzt bringen wir es schön langsam auf den Punkt:
Ein Körper strahlt nicht in allen Frequenzen gleich stark. Die spektrale Verteilung hat irgendwo ihr Maximum. Je kühler ein Körper ist, desto weiter ist dieses Maximum in den energieärmeren Bereich mit kleinen Frequenzen verschoben. Steigt die Temperatur eines Körpers, so "wandert" das Maximum in den energiereicheren Bereich. Bei Temperaturen bis ca. 500 °C ist die Strahlung eines Körpers hauptsächlich Infrarot-Strahlung und wird von uns daher nicht visuell wahrgenommen. Vielmehr spüren wir die Strahlung als Wärme auf unserer Haut. Bei höheren Temperaturen beginnt ein Körper, sogar im für uns sichtbaren Bereich zu strahlen. Er glüht z.B. rötlich (z.B. glühendes Eisen). Je wärmer ein Körper wird, desto "bläulicher" strahlt er.

Analysiert man also das Strahlungsspektrum eines Köpers und macht das Maximum in der spektralen Verteilung ausfindig, kennt man dessen Temperatur. (Dazu muss man halt davon ausgehen, dass sich der Körper annähernd durch einen Schwarzen Strahler beschreiben lässt. Über diese Schwarzkörperstrahlung habe ich hier und hier schon einmal geschrieben.)
Alles was wir also bei ankommendem Sternenlicht tun müssen, ist, sein Licht in die Spektralfarben zu zerlegen und die Intensitäten der verschiedenen Frequenzen (in der Realität: kleine Frequenzintervalle) zu messen. Somit können wir über das sogenannte "Wien'sche Verschiebungsgesetz" die Temperatur errechnen.
Das Wien'sche Verschiebungsgesetz lautet:

λ_max..............Wellenlänge, bei der die Intensität des abgestrahlten Lichts am größten ist

T...................Temperatur des strahlenden Körpers

2897,8 µm·K...Konstante

Das einzige fehlende Glied in dieser Formel ist also die Temperatur - die Wellenlänge mit der größten Intensität (λ_max) kann man ja messen. Ohne Umwege kann man sich so also die Temperatur eines Sterns ausrechnen.

Zur Veranschaulichung dient die folgende Abbildung. Sie zeigt das Spektrum des von unserer Sonne abgestrahlten Lichts ohne den Einfluss der Atmosphäre. (Die Moleküle der Atmosphäre würden bestimmte Frequenzen absorbieren, die dann als Einschnitte in der Kurve sichtbar wären. Mehr dazu im übernächsten Artikel dieser Reihe!)
Man sieht dabei auch schön, warum sich die Sonne annähernd als "Schwarzer Körper" beschreiben lässt: Die transparent graue Fläche skizziert das Schwarzkörper-Spektrum für einen Körper mit der Temperatur 5777 K, während der gelbe Bereich die tatsächlich gemessene Sonnenstrahlung darstellt.

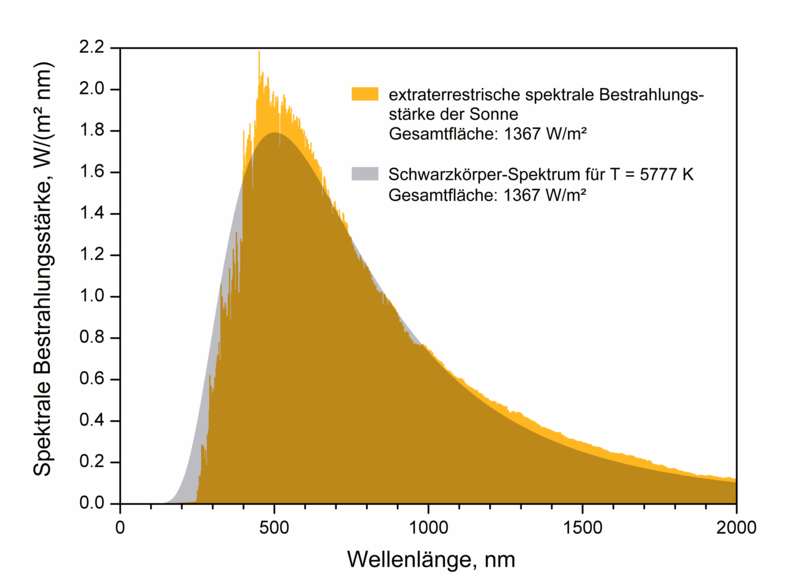Spektrum der Sonne
(Quelle: https://commons.wikimedia.org/wiki/File:EffectiveTemperature_300dpi.png)

Wiegesagt, die Sonne strahlt im visuellen Bereich mit der stärksten Intensität (380-780 nm), was hier eindeutig zu erkennen ist.
Die Oberflächentemperatur der Sonne beträgt ca. 5777 K (also ungefähr 5500 °C). Die Temperaturen anderer bisher analysierter Sterne reichen übrigens ungefähr von 2000 K bis 20000 K.

Wir haben nun also die Möglichkeit der Zerlegung des Lichts in seine Spektralfarben kennengelernt. Der nächste Artikel vertieft diesen Aspekt und erklärt, welche zusätzlichen Informationen man aus einem Lichtspektrum lesen kann. Die Resultate haben u. a. enorme Konsequenzen für unser Verständnis des Universums und unser Weltbild.

Andere Artikel dieser Serie: